Monte Carlo Simulations for Protein Folding
Background
I investigated protein folding with Monte Carlo simulations as part of a problem set at Stanford University.
All structures and graphs shown on this page were generated by code I had written in MATLAB.
The Model
Simple 2D lattice models with hydrophobic or phobic patterning were used to model protein folding. These models are commonly referred to as hydrophobic-polar (HP) models as Lau and Dill studied in 1989.
The potential of the protein structure is defined as:
\[E = -2 \sum_{i<j}^{N} {h_{i,j}} + \sum_{j}^{N} s_{j}\]- $E$ is energy in arbitrary units.
- Interactions between hydrophobic residues are favored:
$ h_{i,j}=1 $ if residues $i$ and $j$ are in nearest neighbor contact, both hydrophobic, and not immediately connected along the chain. Otherwise, $ h_{i,j} = 0 $. - Exposure of hydrophobic residues is disfavored:
$ s_{j}=1 $ is residue $j$ is hydrophobic and in contact with solvent. Otherwise, $ s_{j}=0 $.
Initial Structures
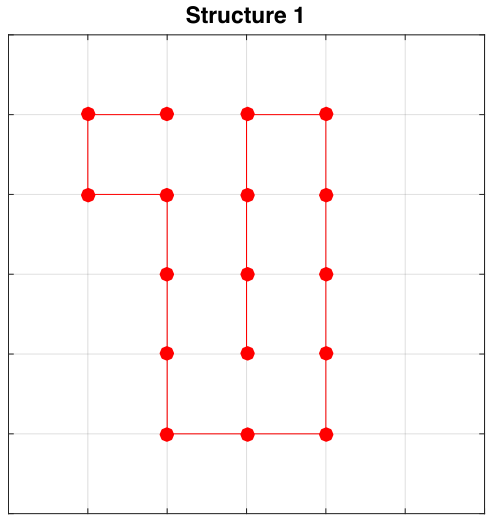
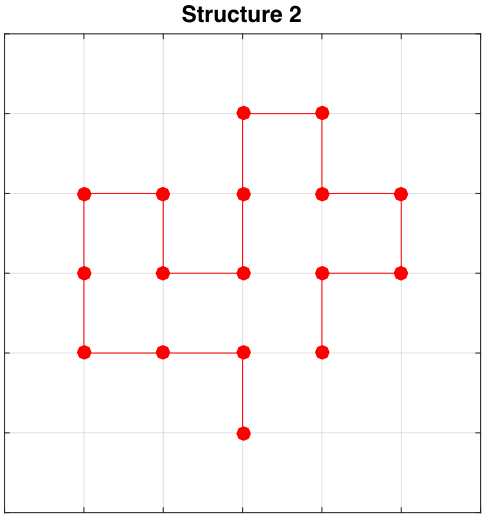
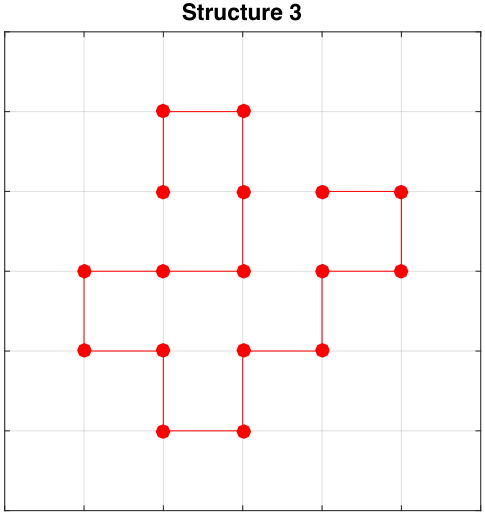
Exploring Sequence Space (Order of Residues)
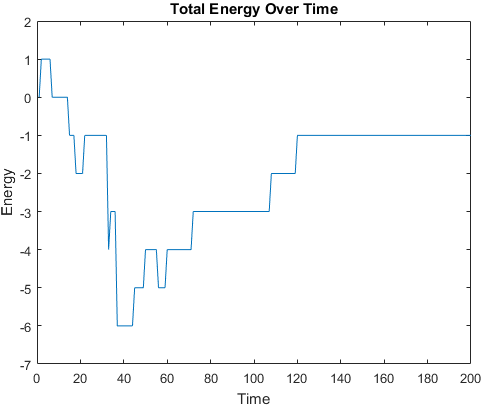
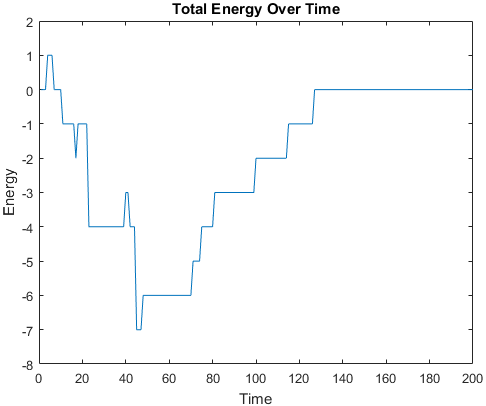
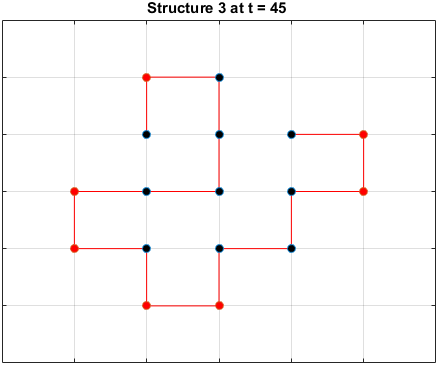
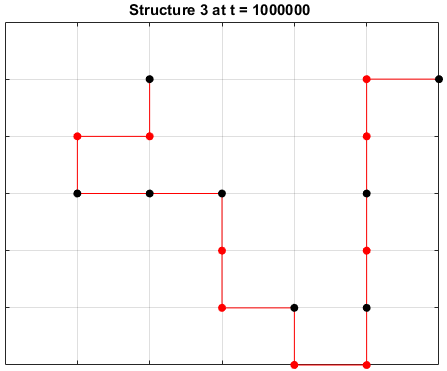
Metropolis Monte Carlo simulations were ran to explore the sequence space of each of the three structures.
In other words, the shape of the structure was kept constant, while the polarity of the residues was perturbed.
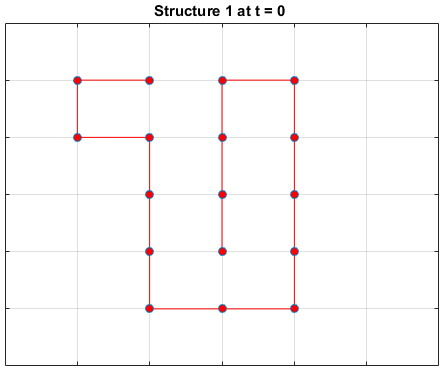
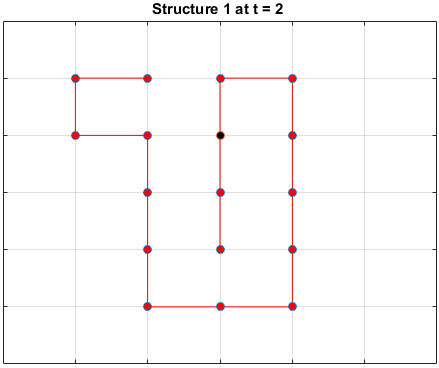
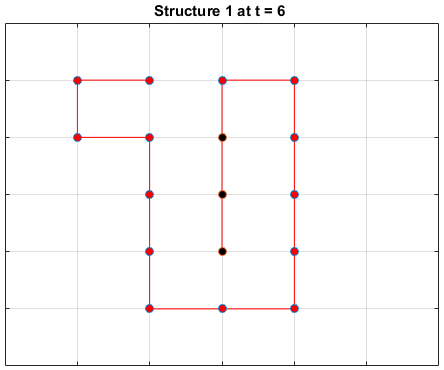
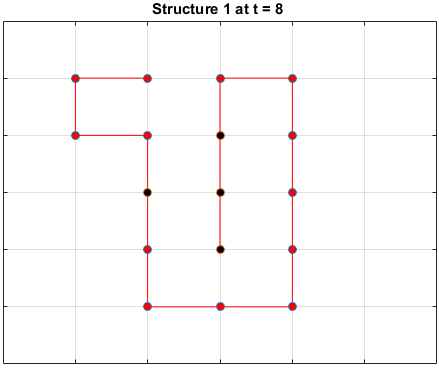
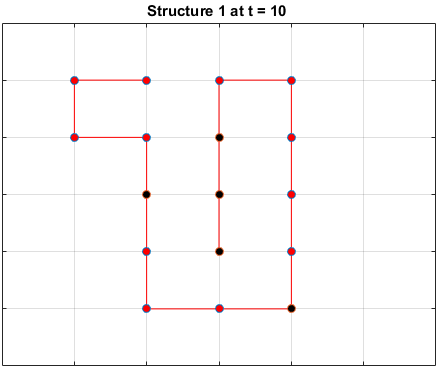
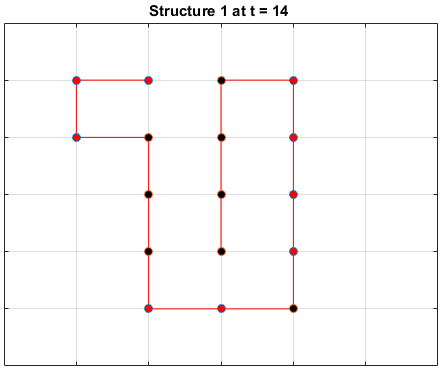
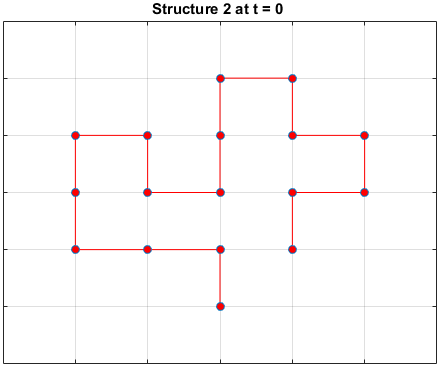
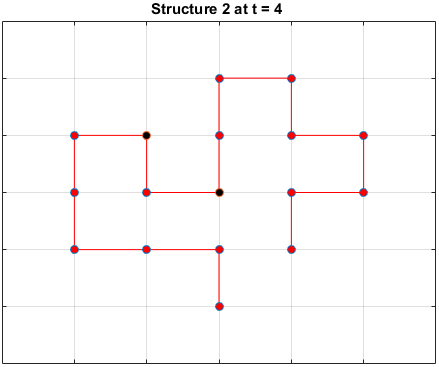
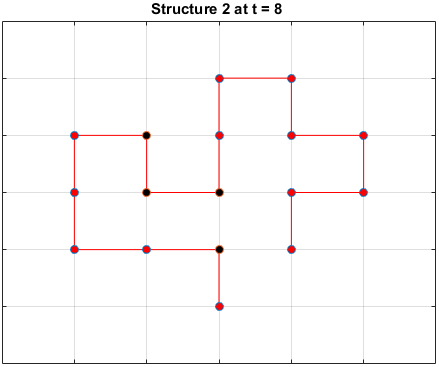
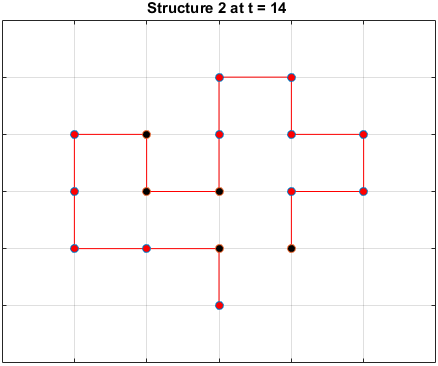
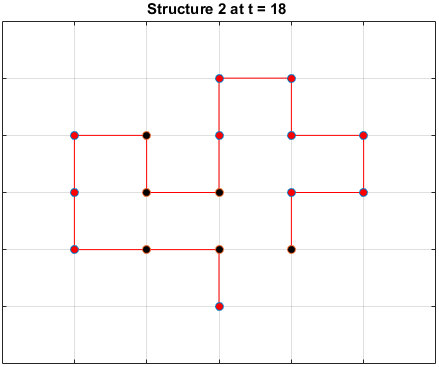
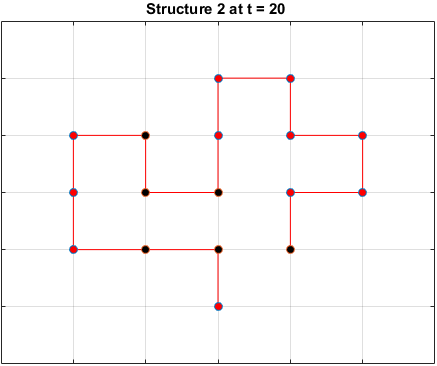
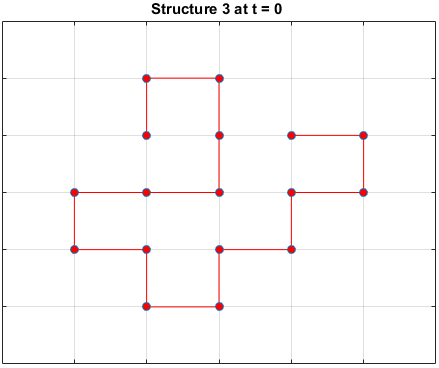
The plots below are examples of a simulation run for each structure.
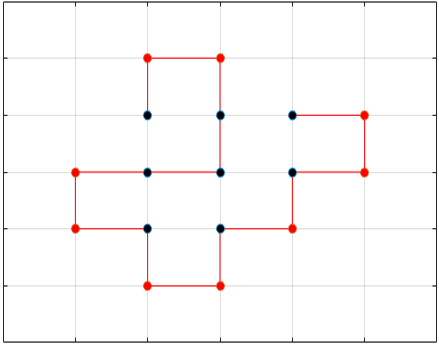
Black dots represent hydrophobic residues and red dots represent polar residues.
Structure 1
Structure 2
Structure 3
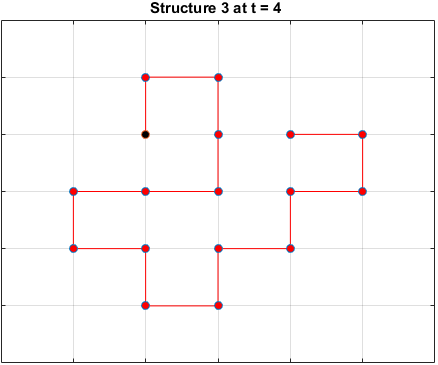
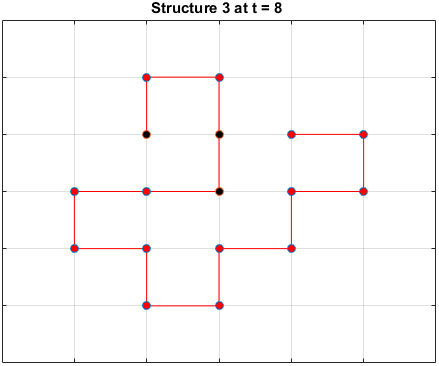
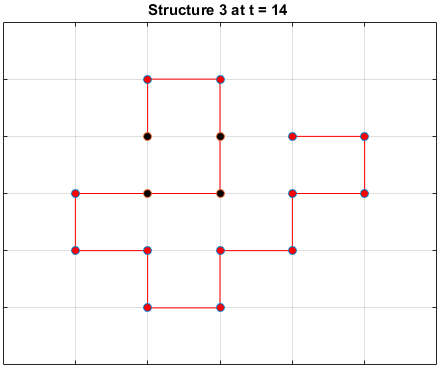
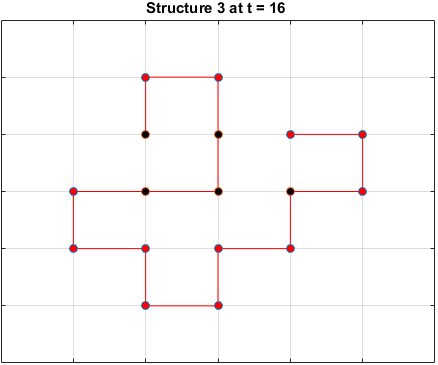
Searching for the Optimal Sequence
MATLAB code from the previous section was adapted to execute $\alpha$ Monte Carlo simulations, each with $\beta$ iterations of random residue.
The code was executed with $\alpha=300$ simulations and $\beta=500$ residue perturbations and the final energy for each simulation result is collected.
The optimal sequence for each structure, i.e. the sequence with the lowest energy, is shown below.
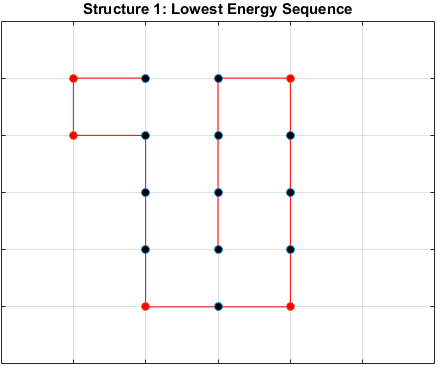
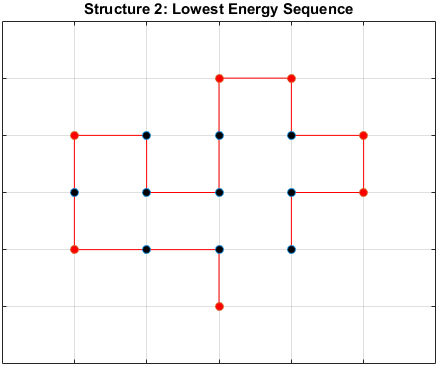
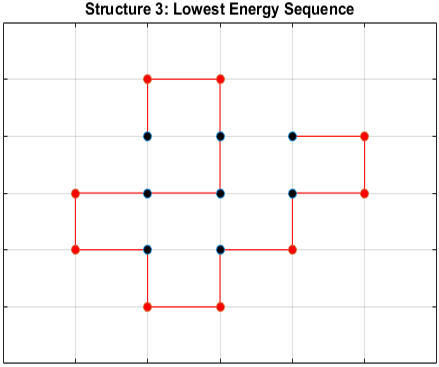



Does the Optimal Sequence Fold Uniquely?
Given the optimal sequences (order of residues) found in the previous section, is it possible for there to be a more optimal structure?
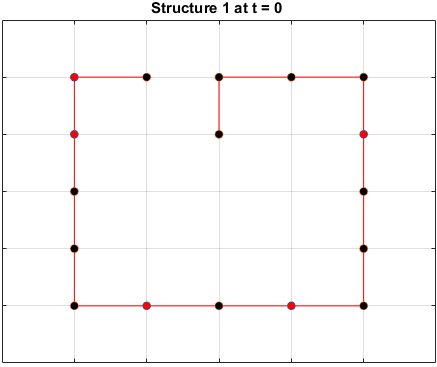
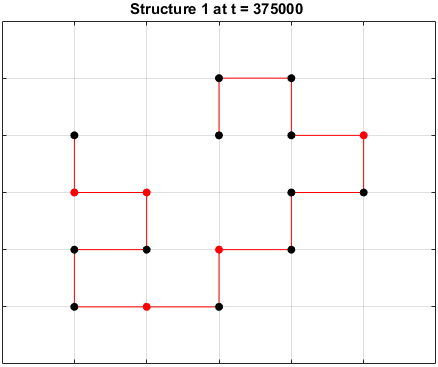
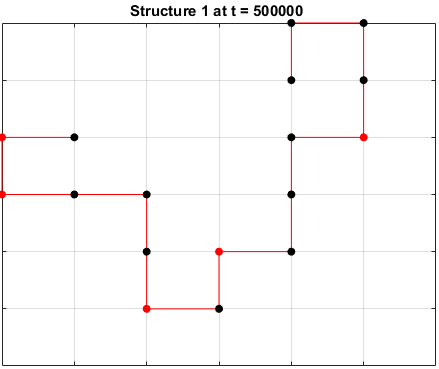
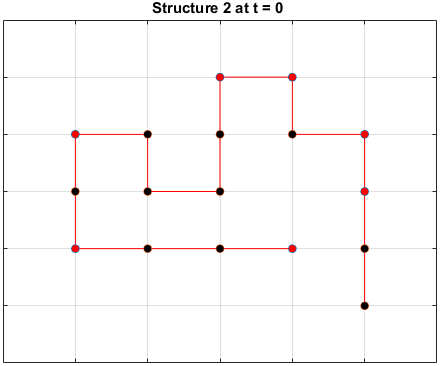
Moveset 1 from “Transition states and folding dynamics of proteins and heteropolymers” from Chan and Dill, 1994, was implemented. The optimal sequences found in the previous section were saved and used in the simulations.
The sequences are given a randomized structure and then folding simulations were ran to see if the structure would fold into a more optimal one.
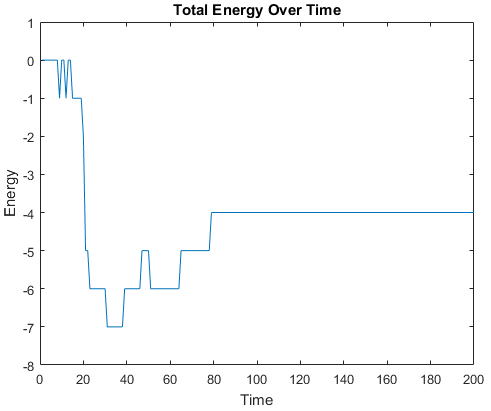
Examples of some folding simluations are shown below.
Sequence 1
Sequence 2
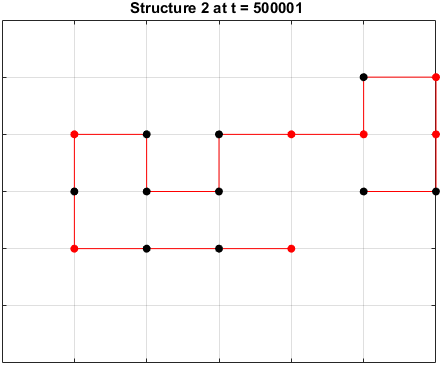
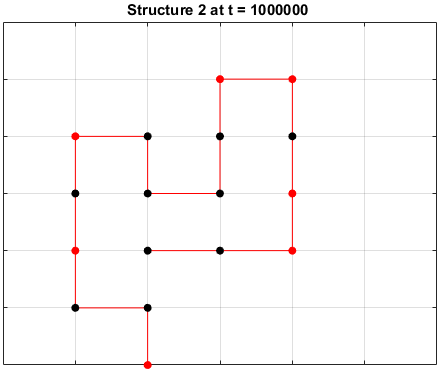
Sequence 3
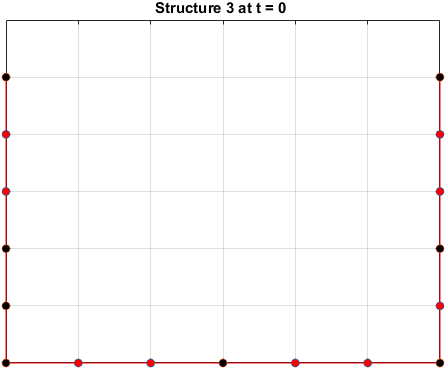
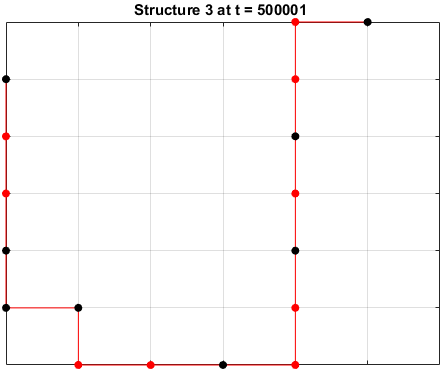
The final results are plotted below. New structures found in the folding
simulations are shown in the top row. The original structure of each sequence
(as found in Searching for the Optimal Sequence) is shown in the bottom row.
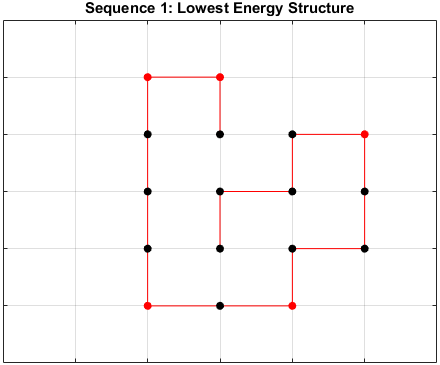
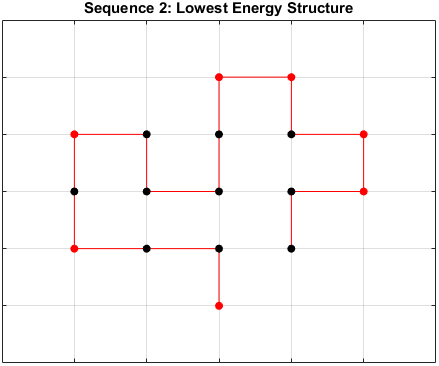
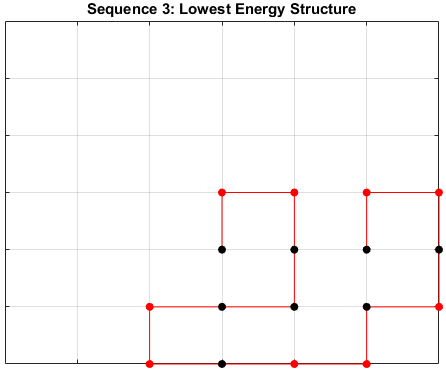
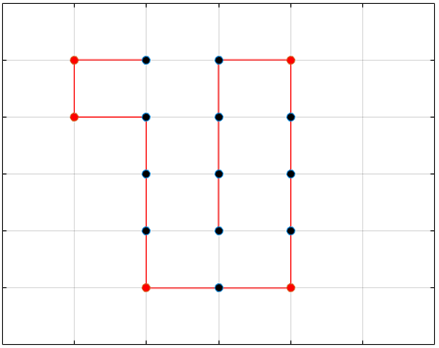
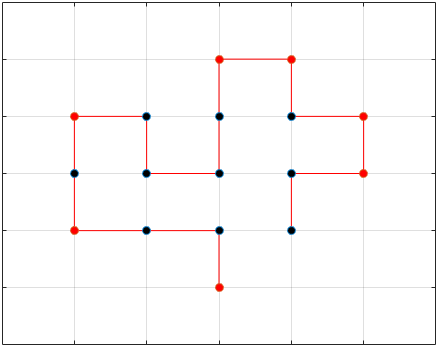

There appears to be a more optimal structure for sequences 1 and 3. Sequence 2 seems to already folded into the most optimal structure.